[Algorithm] 최단경로찾기 - 플로이드 와샬 & 다익스트라
September 18, 2021
플로이드 와샬 알고리즘
존재하는 모든 노드를 최소 비용으로 하나로 연결하는 최단 경로 찾기 알고리즘
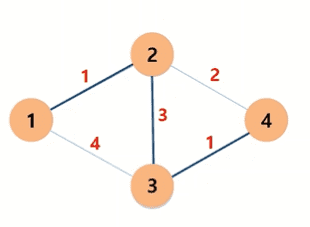
Q. 모든 노드를 연결할 수 있는 최소 비용은 얼마인가?
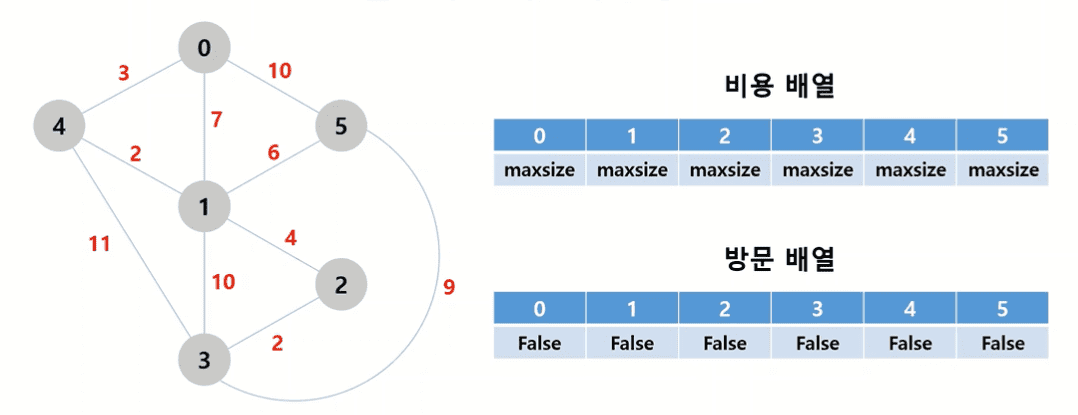
비용 배열과방문 배열을 선언한다. 비용 배열은int값이 가질 수 있는 최대값을, 방문 배열에는 아직 방문하지 않았음을 의미하는False를 담아둔다.- 아무 노드에서나 시작해도 상관없다. 편의상 0번 노드에서 탐색을 시작한다.
- 비용배열의 0번째 인덱스 값을 0번 노드에서 0번 노드까지의 거리인
0으로, 방문배열의 0번째 인덱스 값을True로 갱신한다. - 0번 노드에서 연결할 수 있는 노드는 1, 4, 5번 노드이다. 비용배열의 1, 4, 5번 인덱스 값을 기존값(maxsize)과 비교하여 더 작은 값인
7,3,10으로 각각 갱신한다. - 4번 노드까지의 거리가 최소값이므로 4번으로 이동한다. 방문배열의 4번째 인덱스값을
True로 갱신한다. - 4번 노드에서 아직 방문하지 않았으면서 연결할 수 있는 노드는 1, 3번 노드이다. 비용배열의 1, 3번째 인덱스값을 기존값(7, maxsize)와 비교하여 더 작은 값인
2,11로 각각 갱신한다.
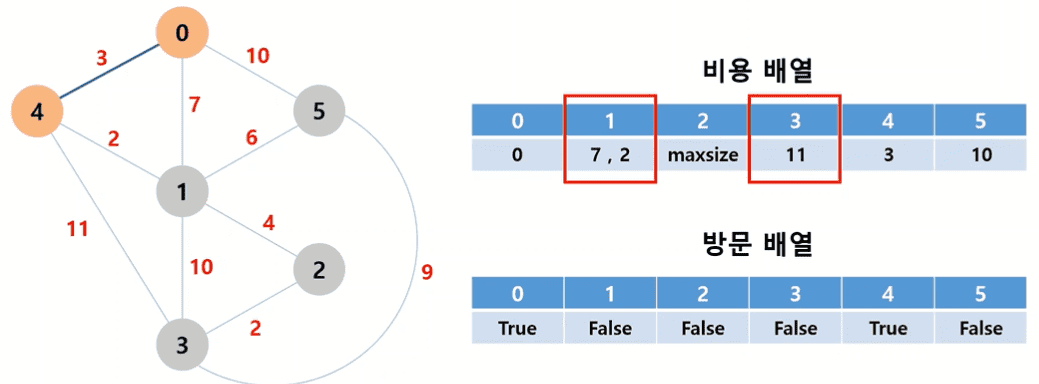
- … 반복 …
- 3번 노드에서 5번 노드까지 갈 수 있으나, 그 비용인
9가 기존값(6)보다 작으므로 갱신되지 않는다.
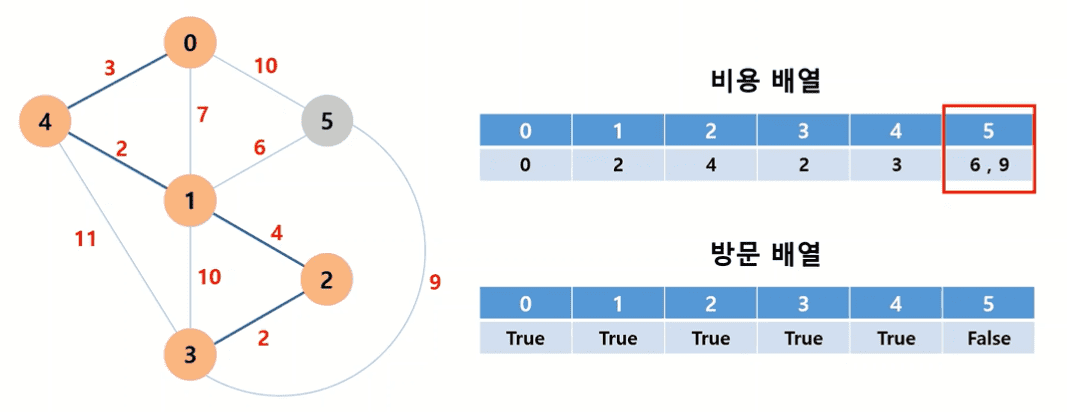
- 마지막 남은 노드인 5번까지 최소 비용으로 연결하고 작업을 종료한다.
- 모든 노드를 연결하는 최소 비용은 0+2+4+2+3+6 = 17 이다.
n = 6 # 노드의 총 개수
costs = [ # [노드a, 노드b, a에서 b로 이동하는 비용]
[0,1,7],
[0,4,3],
[0,5,10],
[1,2,4],
[1,3,10],
[1,4,2],
[1,5,6],
[2,3,2],
[3,4,11],
[3,5,9]
]
def solution(costs):
values = [2**31-1 for _ in range(n)] # 비용 배열 : int의 최대값으로 초기 설정
visited = [False for _ in range(n)] # 방문 배열 : False로 초기 설정
answer = 0
start = 0 # 0번 노드에서 시작
visited[start] = True
values[start] = 0
while False in visited:
# 노드 완전탐색으로 비용배열의 값을 최소값으로 갱신
for i in costs:
if visited[i[1]] == False and i[0] == start: # i[0]에서 i[1]로 가는 경우
values[i[1]] = min(values[i[1]], i[2])
if visited[i[0]] == False and i[1] == start: # i[1]에서 i[0]로 가는 경우
values[i[0]] = min(values[i[0]], i[2])
# 방문하지 않은 노드 중 최소 비용으로 갈 수 있는 노드 탐색
refer = 2**31-1
for i in range(n):
if visited[i] == False and values[i] != 0:
refer = min(refer, values[i])
answer += refer
# 해당 노드 방문 체크
for i in range(n):
if visited[i] == False and values[i] == refer:
visited[i] = True
start = i # 현재 노드를 i로 이동한 후 while문 재실행
break
return answer다익스트라 알고리즘
특정 노드에서 다른 노드까지의 최단 경로를 찾는 알고리즘
💡 동작 원리
- 출발 노드를 설정한다
- 비용 리스트를 (무한으로) 초기화한다
- 방문하지 않은 노드 중 최단 거리가 가장 짧은 노드를 선택한다
- 해당 노드를 거쳐 다음 노드로 가는 비용을 계산한다. 다음 노드로 가는 비용을 기존에 구해놓은 값이 있다면, 새로 구한 값과 기존값중 최소값으로 비용 리스트를 갱신한다
- 3~4번 과정을 반복한다
예: 1번 노드에서 4번 노드까지의 최단경로 찾기
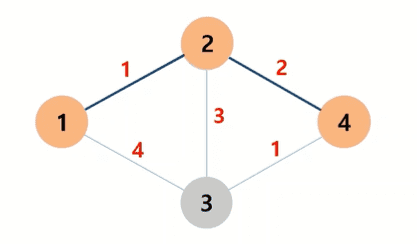
Q. 0번 노드에서 n번 노드까지 연결하는 최소 비용은 얼마인가?

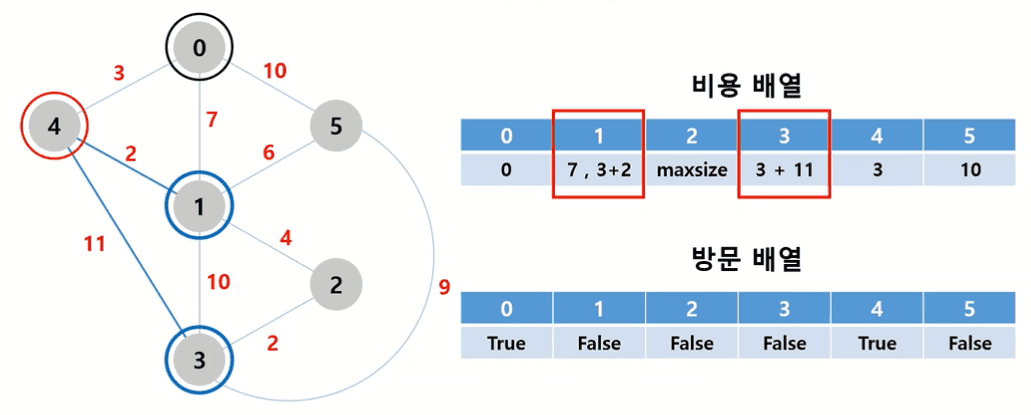
비용 배열과방문 배열을 선언한다. 비용 배열은int값이 가질 수 있는 최대값을, 방문 배열에는 아직 방문하지 않았음을 의미하는False를 담아둔다.- 비용배열의 0번째 인덱스 값을 0번 노드에서 0번 노드까지의 거리인
0으로, 방문배열의 0번째 인덱스 값을True로 갱신한다. - 0번 노드에서 연결할 수 있는 노드는 1, 4, 5번 노드이다. 비용배열의 1, 4, 5번 인덱스 값을 기존값(maxsize)과 비교하여 더 작은 값인
7,3,10으로 각각 갱신한다. - 4번 노드까지의 거리가 최소값이므로, 방문배열의 4번째 인덱스값을
True로 갱신한다. - 4번 노드에서 아직 방문하지 않았으면서 연결할 수 있는 노드는 1, 3번 노드이다. 그런데 1번 노드까지 가는 길은 0번에서 4번을 거쳐서 1번으로 가는 방법도 있지만(비용 3+2 = 5), 아까 계산해놓은 0번에서 1번으로 바로 가는 방법도 있다(비용 7). ⚡즉, 다익스트라 알고리즘에서는 현재 노드까지 오는 비용에 새로운 노드로 가는 비용을 누적하고, 그 누적값을 기존값과 비교하여 최소값으로 갱신한다. ⚡ 따라서 1번 노드로 가는 비용은 3+2=5와 기존값(7) 중 최솟값인
5로 갱신한다. 3번으로 가는 비용은 3+11 = 14와 기존값(maxsize) 중 최솟값인14로 갱신한다. 비용 갱신을 마친 후 탐색을 종료한다.
- 아직 방문하지 않은 1, 2, 3, 5번 노드 중에서 비용 최소값을 갖는 1번 노드에서 탐색을 시작한다. 1번 노드를 방문했음을 표시하기 위해 방문배열의 1번인덱스 값을
True로 변경한다. - 1번 노드에서 아직 방문하지 않았으면서 연결할 수 있는 노드는 2, 3, 5번이다. 1번 노드까지 오는 비용(5)에 새로 연결될 노드까지 가는 비용 4, 10, 6을 더한 9, 15, 11을 기존 비용(maxsize, 14, 10)과 비교하여, 둘 중 최소값인
9,14,10으로 각각 갱신한다. 비용 갱신을 마친 후 탐색을 종료한다. - … 반복 …
- 마지막으로 방문하지 않은 3번 노드에서 탐색을 시작한다. 아직 방문하지 않았으면서 연결할 수 있는 노드가 더이상 없으므로 알고리즘을 종료한다.
- 최종적으로 비용배열 values의 원소 values[i]는 0번 노드에서 i번 노드로 가는 최소 비용이 된다.
import sys
n = 6
costs = [
[0,1,7],
[0,4,3],
[0,5,10],
[1,2,4],
[1,3,10],
[1,4,2],
[1,5,6],
[2,3,2],
[3,4,11],
[3,5,9]
]
def solution(costs):
values = [sys.maxsize for _ in range(n)] # 비용 배열 : int의 최대값으로 초기 설정
visited = [False for _ in range(n)] # 방문 배열 : False로 초기 설정
start = 0 # 시작 노드
values[start] = 0
while False in visited:
# 탐색하지 않은 노드 찾기
checkLoc = -1 # 탐색할 노드를 담을 변수
checkValue = sys.maxsize # 해당 노드까지 가는 비용을 담을 변수
for i in range(n):
if visited[i] == False and values[i] < checkValue: # for문을 돌면서 방문하지 않은 노드 중 비용 최솟값을 갖는 노드를 선택
checkLoc = i
checkValue = values[i]
# 탐색하지 않은 노드가 없다면(for문 다 돌았는데 checkLoc가 바뀌지 않음) while문 종료
if checkLoc == -1:
break
# 경로 완전탐색으로 비용배열 갱신
visited[checkLoc] = True
for v1, v2, c in costs:
if v1 == checkLoc and visited[v2] == False: # v1에서 v2로 가는 경우
values[v2] = min(values[v2], values[v1]+c)
if v2 == checkLoc and visited[v1] == False: # v2에서 v1로 가는 경우
values[v1] = min(values[v1], values[v2]+c)
return values