[Algorithm] 그리디(Greedy) 알고리즘
September 30, 2021
탐욕법(Greedy Algorithm)?
전체가 아닌 현재 상태에서 최선의 선택을 하는 알고리즘.
전체탐색보다 빠르지만 반드시 정답을 도출하지는 않는다.
전체 문제를 작은 문제로 나누어서 정답을 구한다는 점에서 동적계획법과 유사하지만, 작은 문제들의 최적의 해가 전체의 최적의 해가 될 수 있는지 판단해서 탐욕법이 적용가능한지 우선 판단해야 한다.
탐욕법을 쓸 수 있는 조건
Greedy choice property: 각 부분에서의 선택이 다른 부분에게 영향을 주지 않는다.Optimal substructure: 각 부분에서의 최적해가 전체의 최적해이다.
⚡ 아래와 같은 최단경로탐색에서 1번 선택은 2번 선택에 영향을 준다 ➡ 동적계획법 사용
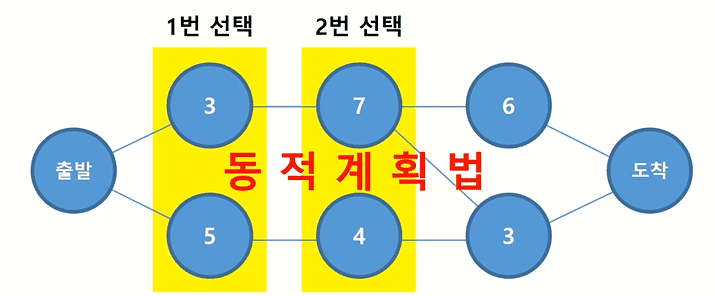
⚡ 아래와 같은 최단경로탐색에서는 1번 선택과 상관없이 2번 선택을 할 수 있다 ➡ 탐욕법 사용 가능
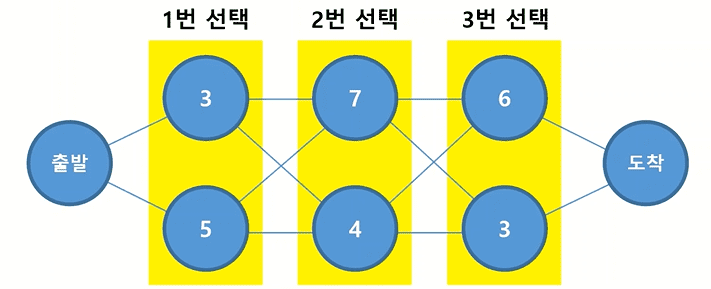
탐욕법 예제
1) 교환 가능한 동전의 최소 갯수 구하기
Q1 ) 500원, 100원, 50원, 10원을 사용해 1,970원 만들기
- 동전들이 서로간 배수이므로 탐욕법 적용 가능
- 매 순간의 최적의 해의 합이 전체의 최적의 해가 된다.
coin = [500, 100, 50, 10]
n = 1970
cnt = 0
for c in coin:
cnt += n // c # 가장 큰 화폐단위부터 최대로 사용한다 (순간순간의 최적의 해를 구한다)
n %= c # n값을 c로 나누고 남은 나머지값으로 바꿔주고 반복문 진행
print(cnt) # 매 순간의 최적해의 합 = 정답Q2 ) 500원, 300원, 200원, 50원, 10원을 사용해 1,970원 만들기
- 500원 3개 + 300원 1개 + 200원 0개 + 50원 3개 + 10원 2개 => 총 9개
-
그러나 탐욕법을 따르지 않고 500원 3개 + 300원 0개 + 200원 2개 + 50원 1개 + 10원 2개를 사용한다면? => 총 8개의 동전만 사용해도 된다
- 300원이 200원의 배수가 아니기 때문에 300원 선택의 순간이 200원 선택 순간에 영향을 미친다 => 탐욕법 적용 불가
2) 가능한 많은 수의 회의시간
Q) 하나의 회의실을 여러 팀이 사용하고자 할때, 최대한 많은 팀이 회의실을 사용할 수 있도록 회의시간 배치하기
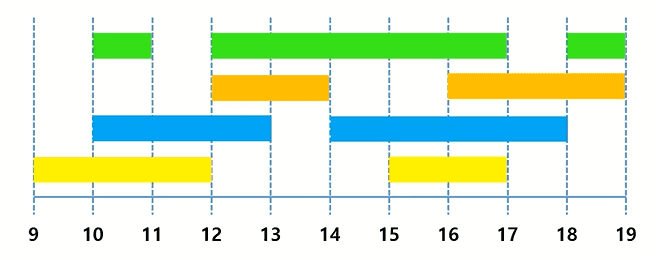
meetings = [
[9,12],
[10,11],
[10,13],
[12,14],
[12,17],
[14,18],
[15,17],
[16,19],
[18,19]
]3) 카드게임
Q) 서로 한장씩 카드를 뽑아 비교했을 때 더 큰 숫자를 뽑은 사람이 점수를 획득한다. A가 얻을 수 있는 최대 점수는?